Hey guys!
Here you can find all types notes by handwritten.
Here,we are providing physics E.M.F.
effect,which is most useful in your semester exam.This topic is totally designed according to our syllabus.
effect,which is most useful in your semester exam.This topic is totally designed according to our syllabus.
#This all topic will be covered in video lecture form on my youtube chanel.
Youtube Link:-
EMF Equation of a Transformer
When a sinusoidal voltage is applied to the primary winding of a transformer, alternating flux ϕm sets up in the iron core of the transformer. This sinusoidal flux links with both primary and secondary winding. The function of flux is a sine function.
The rate of change of flux with respect to time is derived mathematically.
The derivation of the EMF Equation of the transformer is shown below. Let
- ϕm be the maximum value of flux in Weber
- f be the supply frequency in Hz
- N1 is the number of turns in the primary winding
- N2 is the number of turns in the secondary winding
Φ is the flux per turn in Weber
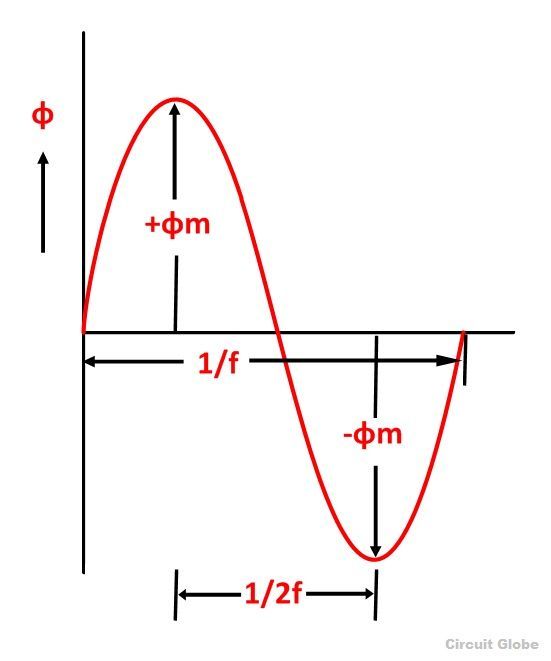 As shown in the above figure that the flux changes from + ϕm to – ϕm in half a cycle of 1/2f seconds.
As shown in the above figure that the flux changes from + ϕm to – ϕm in half a cycle of 1/2f seconds.
 As shown in the above figure that the flux changes from + ϕm to – ϕm in half a cycle of 1/2f seconds.
As shown in the above figure that the flux changes from + ϕm to – ϕm in half a cycle of 1/2f seconds.
By Faraday’s Law
So the induced emf lags flux by 90 degrees.
The above equation is called the turn ratio where K is known as the transformation ratio.
The equation (8) and (9) can also be written as shown below using the relation



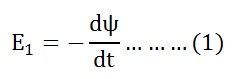
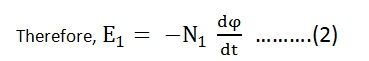
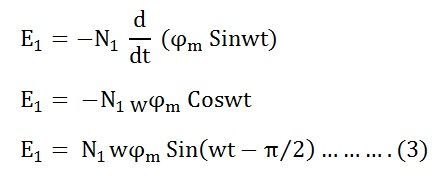
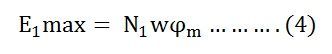
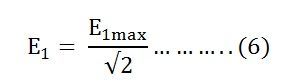
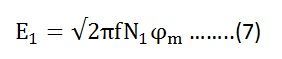

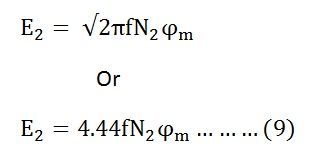
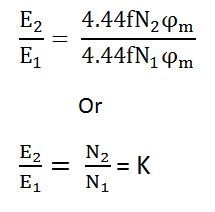
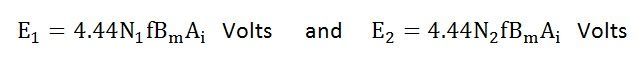
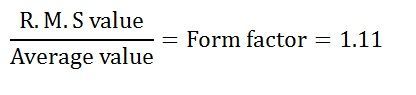




0 Comments
If you have any doubts,please let me know.